This posting contains large animations.
Given a polynomial $p(x,y): \mathbb{R}^2 \to \mathbb{R}$ of degree $3$, a cubic is defined to be the plane curve
$$\{(x,y) \in \mathbb{R}^2 : p(x,y) = 0\}.$$
The same way, we define a quadratic or conic to be a second-order plane curve. Now suppose that we have two cubics, defined by $p_1$ and $p_2$, respectively, and a conic, given by $q$. Then by Bézout’s theorem, the cubics intersect in at most $9$ points. By the same theorem, both cubics intersect with the conic in at most $6$ points. We have $18$ degrees of freedom, of which we spend $12$ to request the two cubics to intersect at exactly $6$ points lying on the conic, and we use the remaining $6$ degrees to force the cubics to intersect in exactly $3$ more points in the plane.
This construction makes sure that $p_1$, $p_2$, and $q$ do not share a common component. We introduce one more degree of freedom by taking a linear combination of $p_1$ and $p_2$, say $\beta p_1 + (1-\beta) p_2$, and we fix this new parameter by claiming the additional condition
$$\beta p_1(x_0,y_0) + (1-\beta) p_2(x_0,y_0) = 0$$
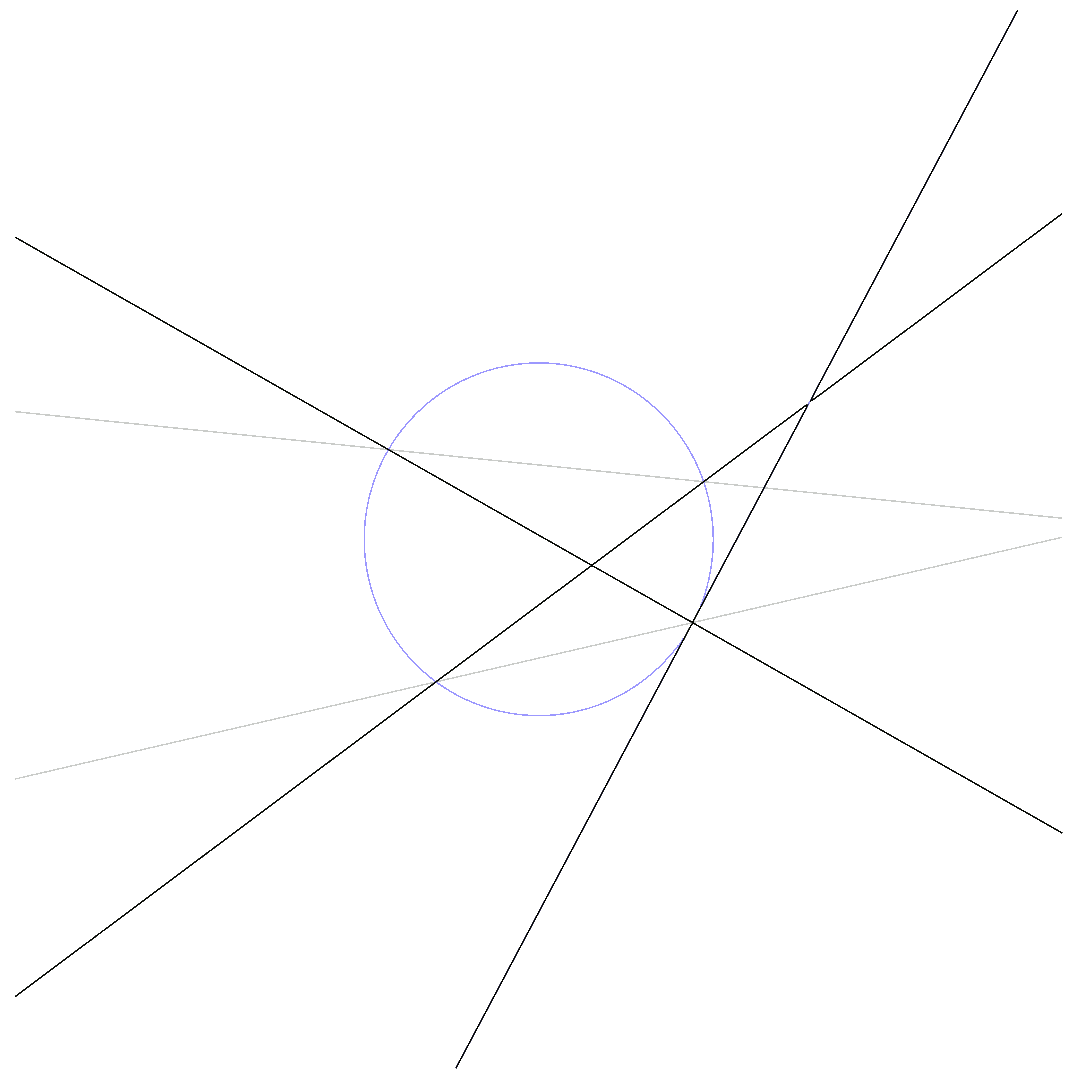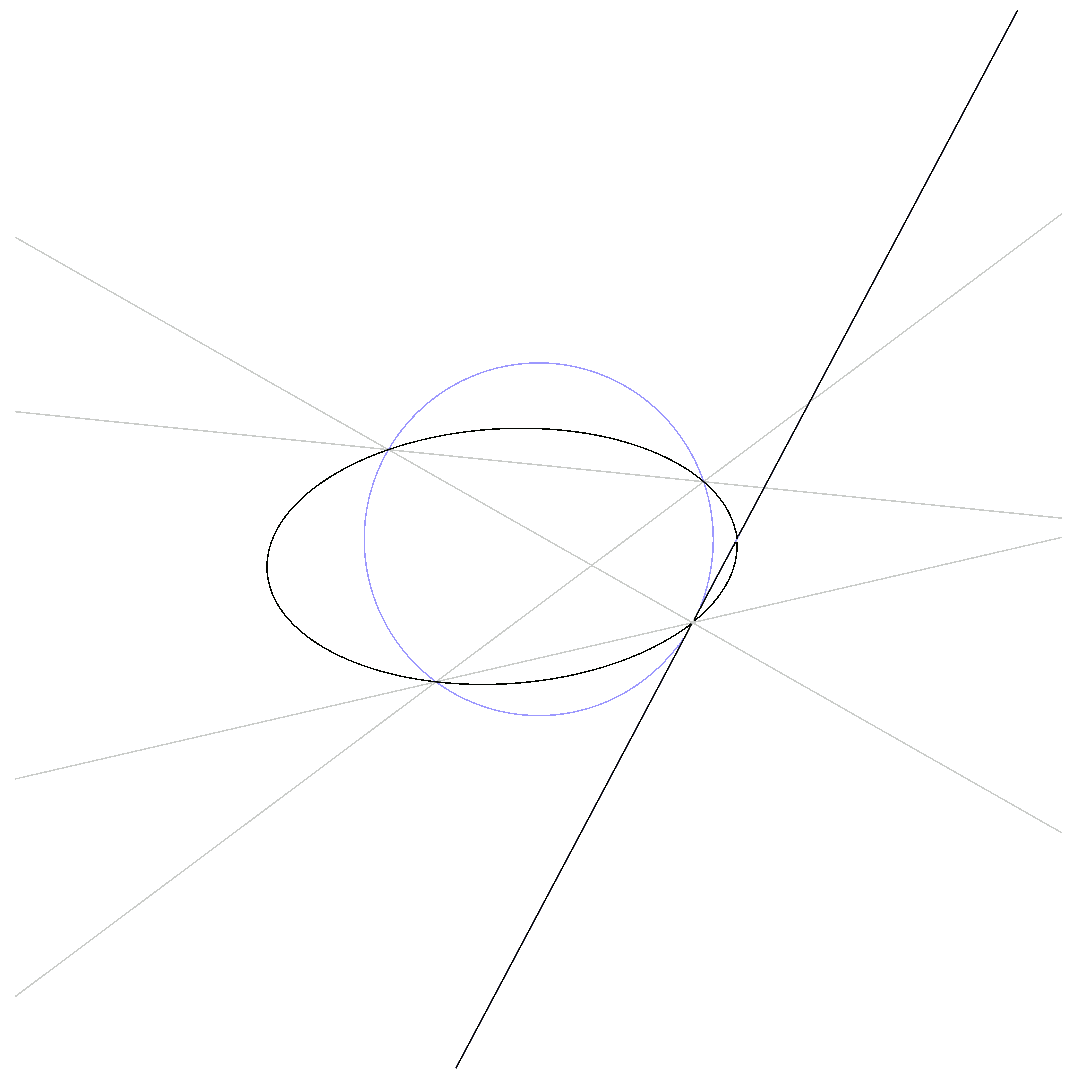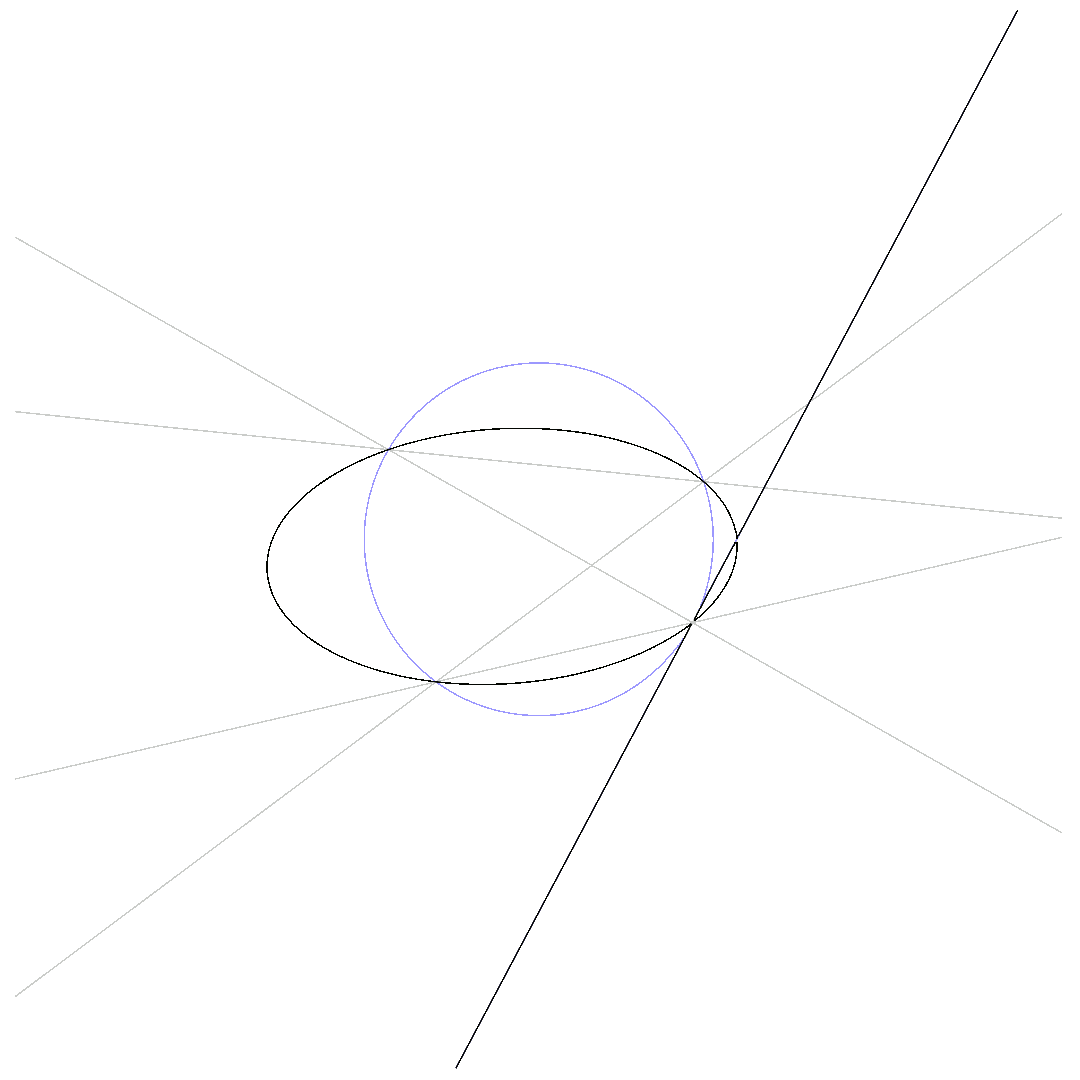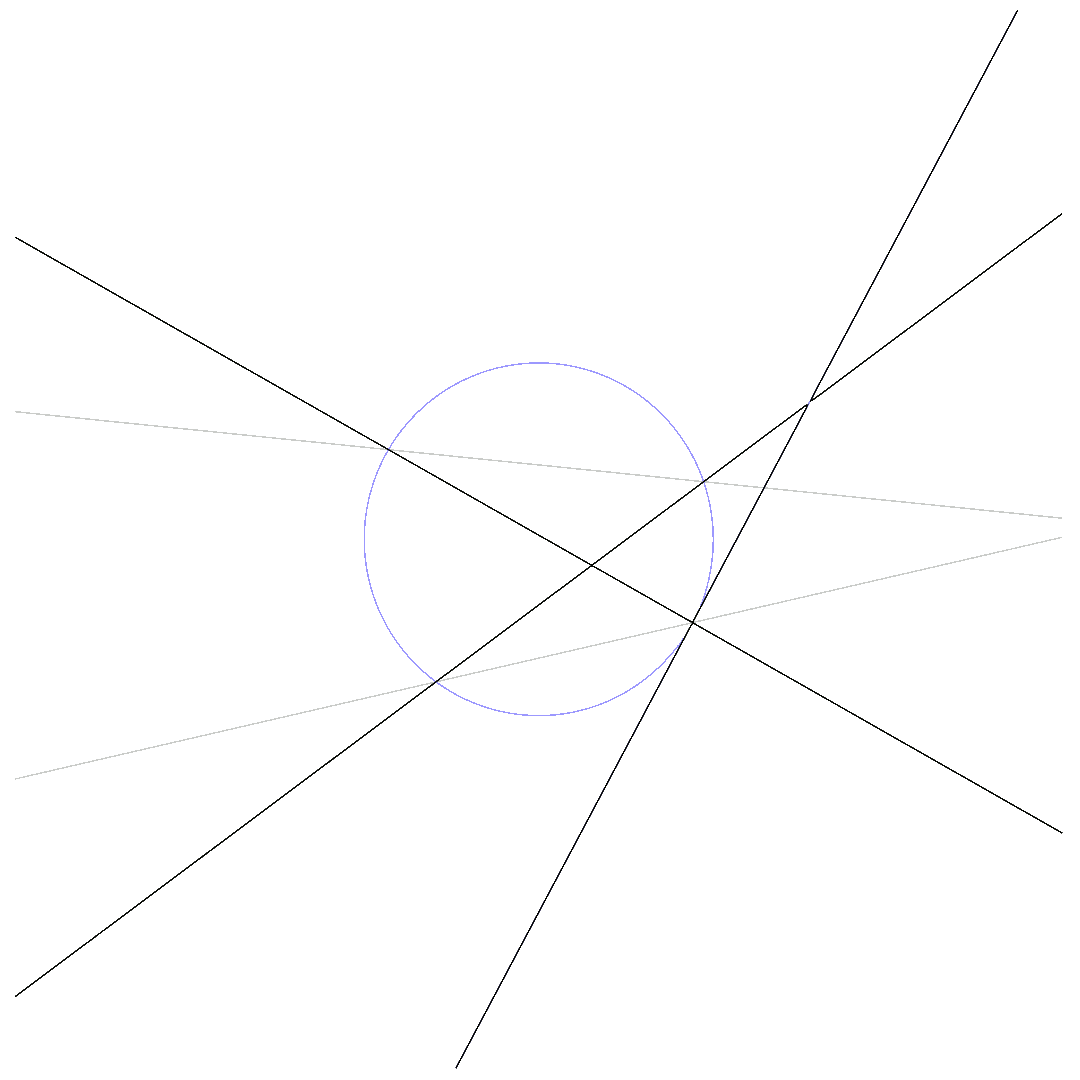
for some $(x_0,y_0)$ satisfying $q(x_0,y_0) = 0$. As an effect, the curve defined by $\beta p_1(x,y) + (1-\beta) p_2(x,y) = 0$ and the conic now intersect in $7$ points, but the linear combination of $p_1$ and $p_2$ still defines a cubic, which, again due to Bézout’s theorem, is only possible if $\beta p_1 + (1-\beta) p_2$ and $q$ share a common component. This component can only be $q$ itself, so that there exists an affine function $l$ such that
$$\beta p_1 + (1-\beta)p_2 = q \cdot l$$
This proves Pascal’s and Pappus’ (here, $q = s \cdot t$ with affine functions $s$ and $t$) theorem at the same time, as it says that the $3$ points outside the conic are collinear, that is, they are located on the same line, the Pascal-line.
The animations below show how $p_1 = 0$ deforms to $p_2 = 0$ for $\beta$ running from $0$ to $1$ while passing through $q\cdot l = 0$.
The so-called 6-point-Pascal consists of 6 distinct points on the conic.
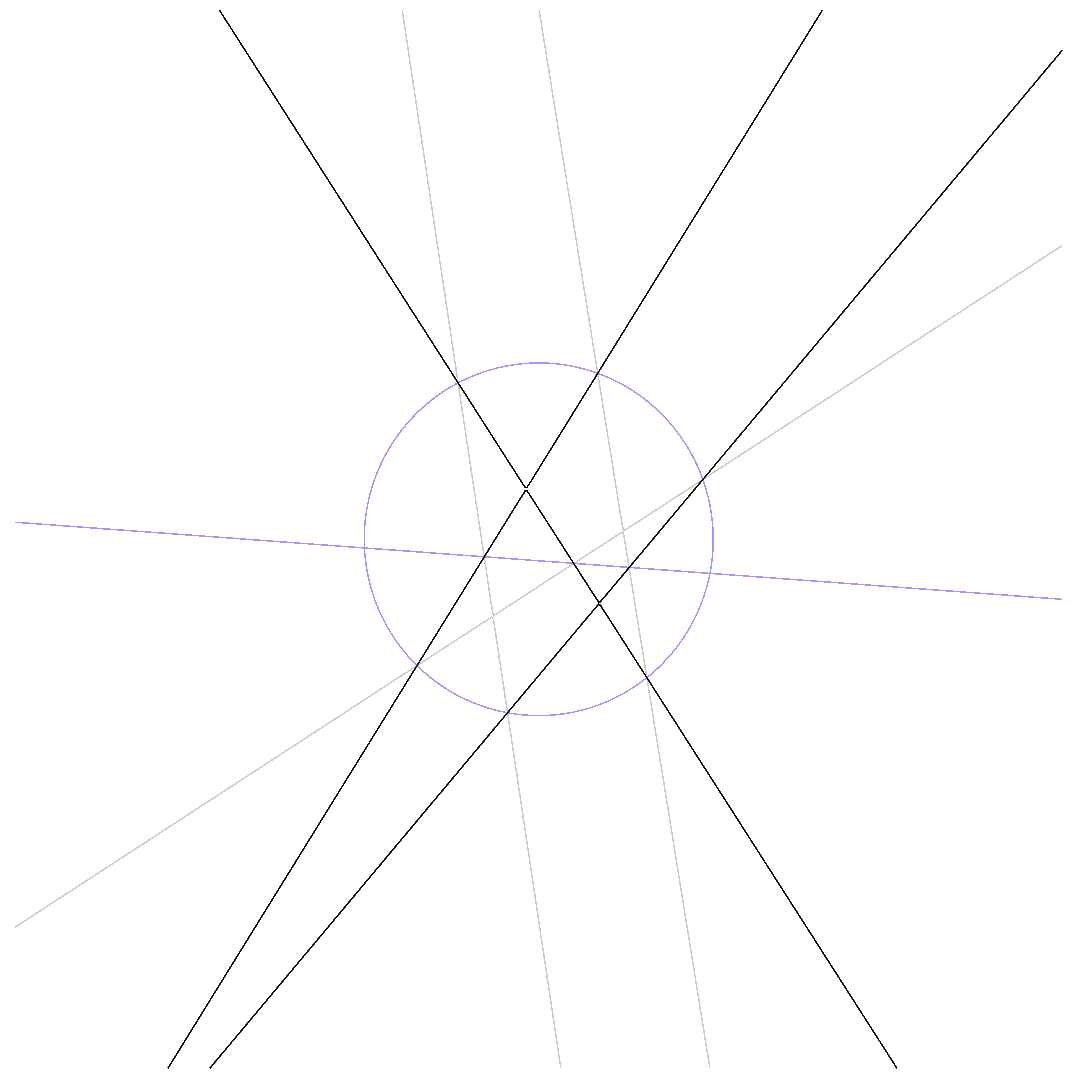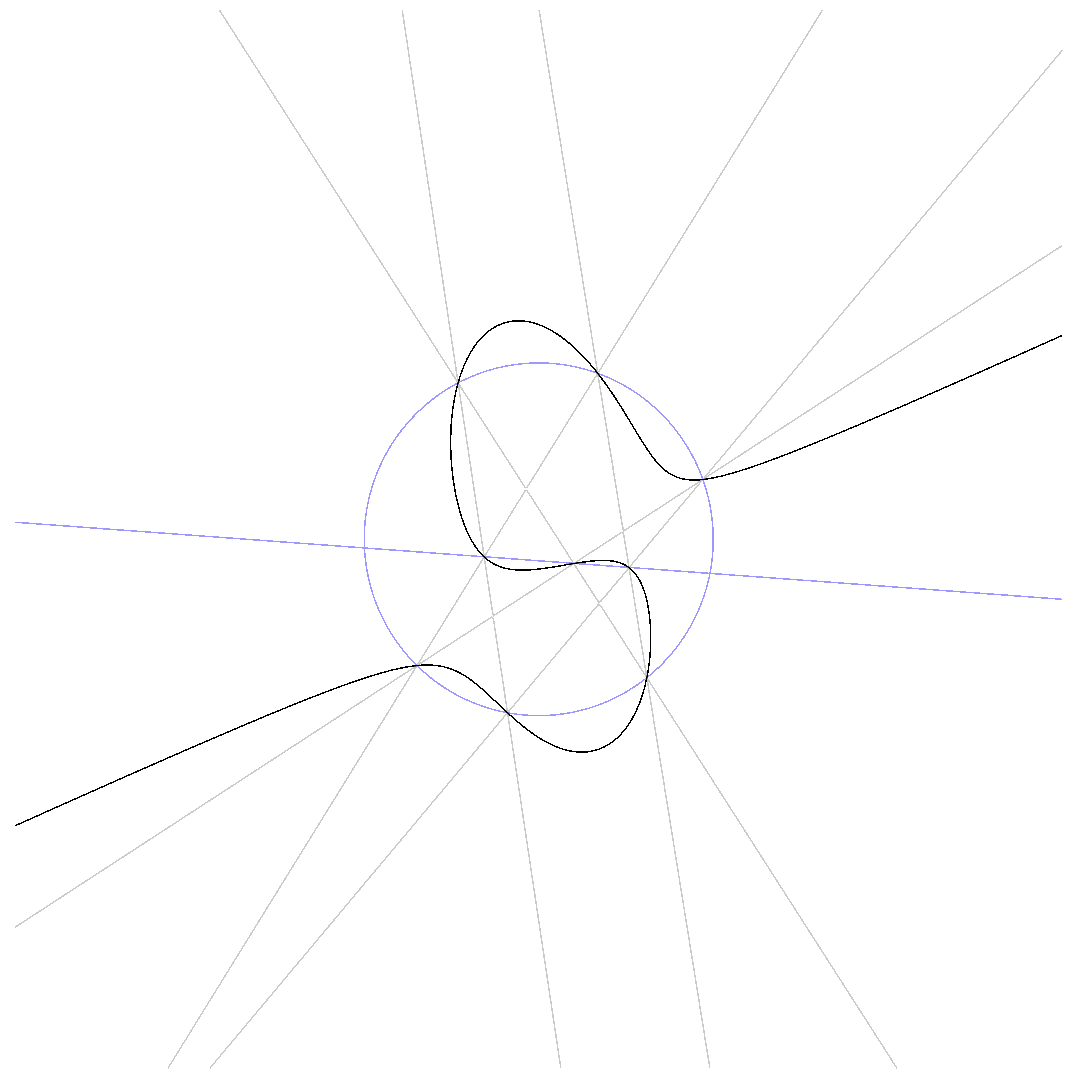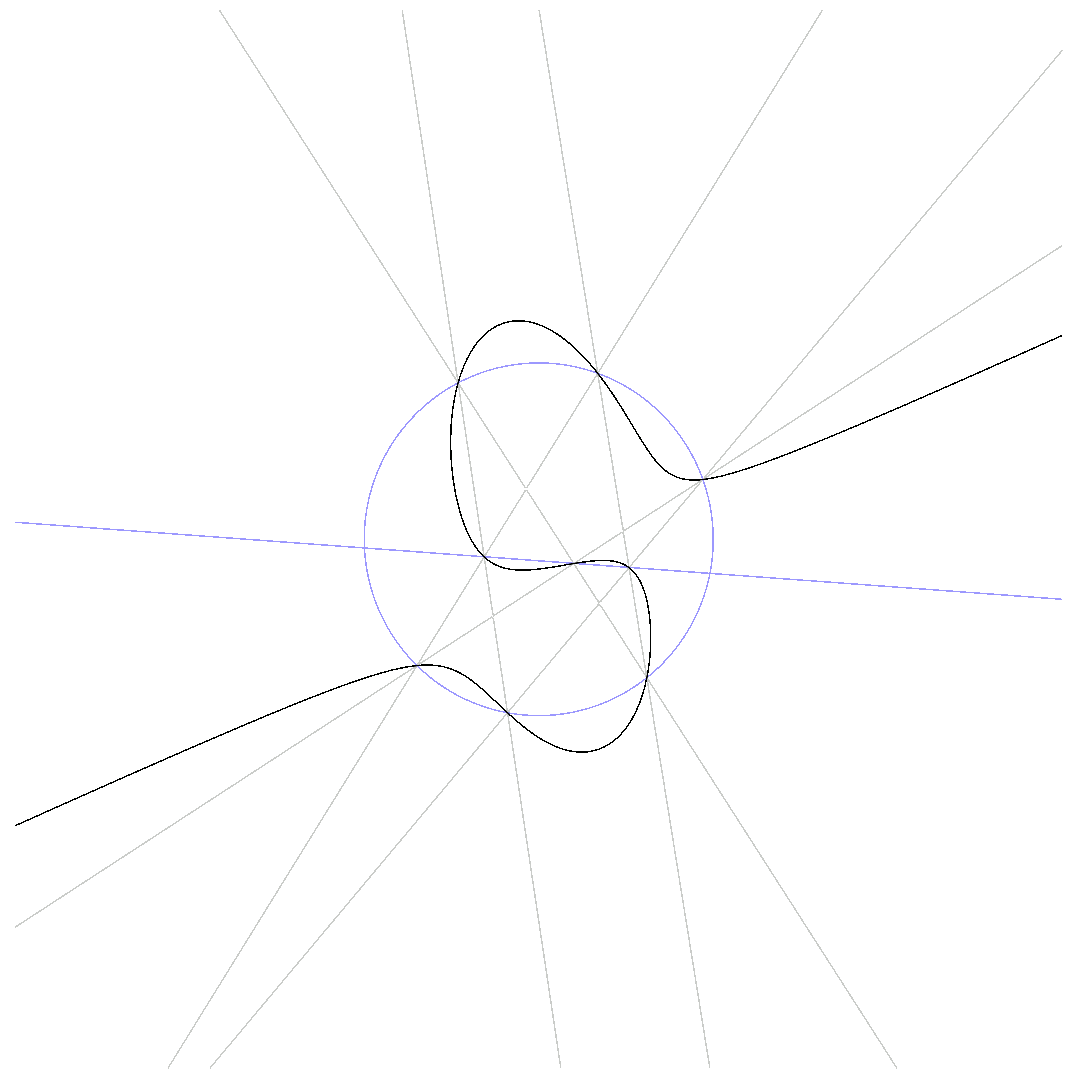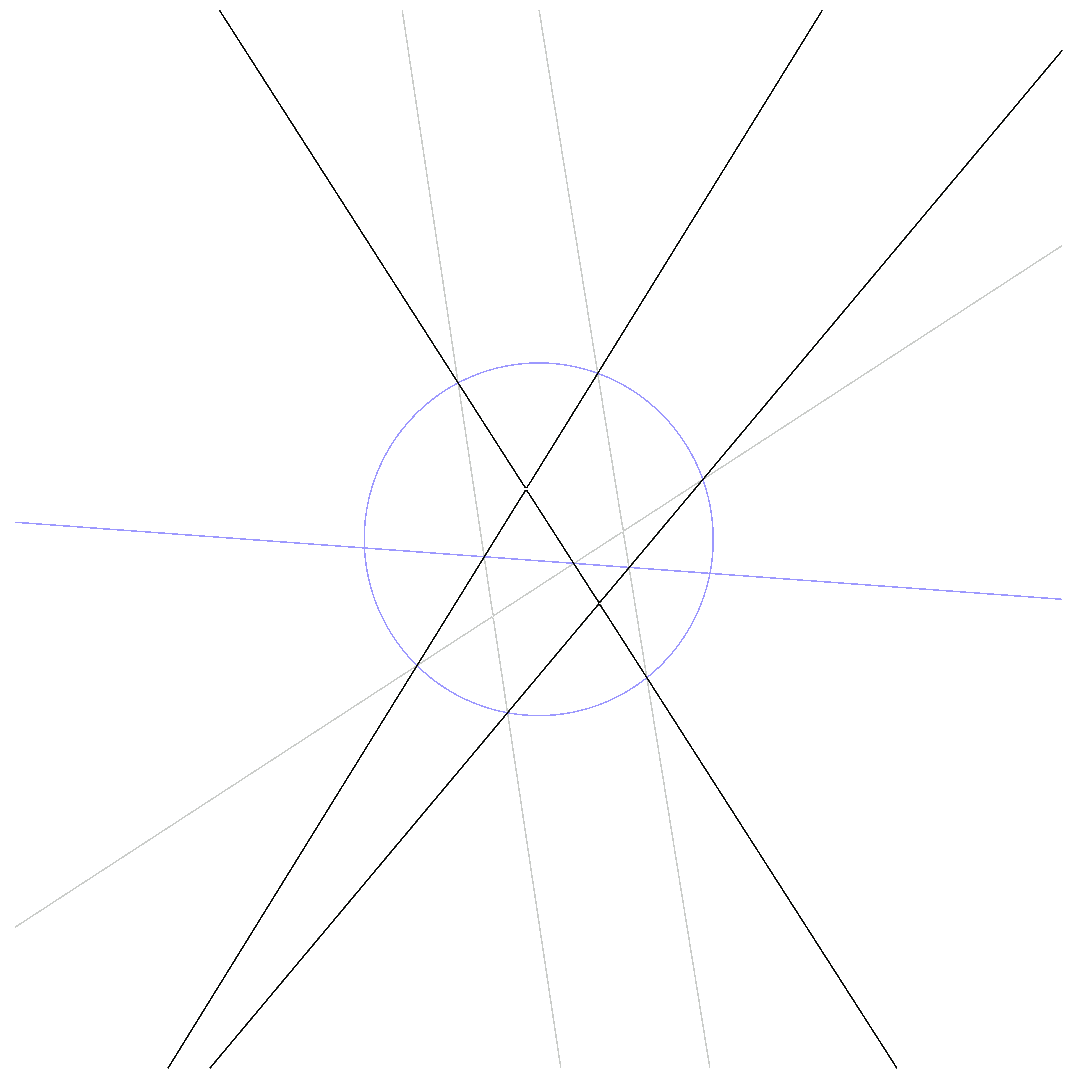
$\mbox{Pascal-line passes through conic}$
The Pascal-line does not need to pass the conic.
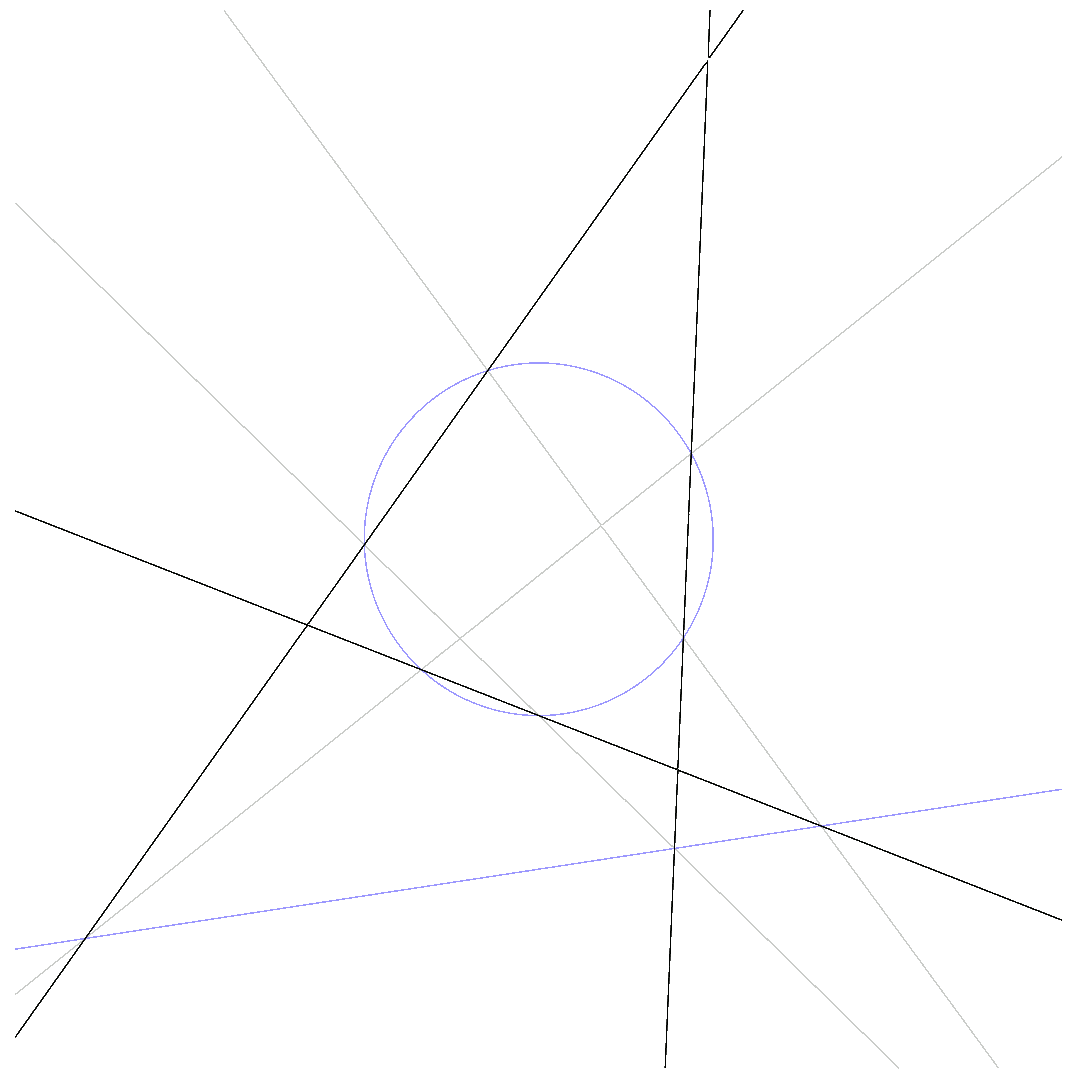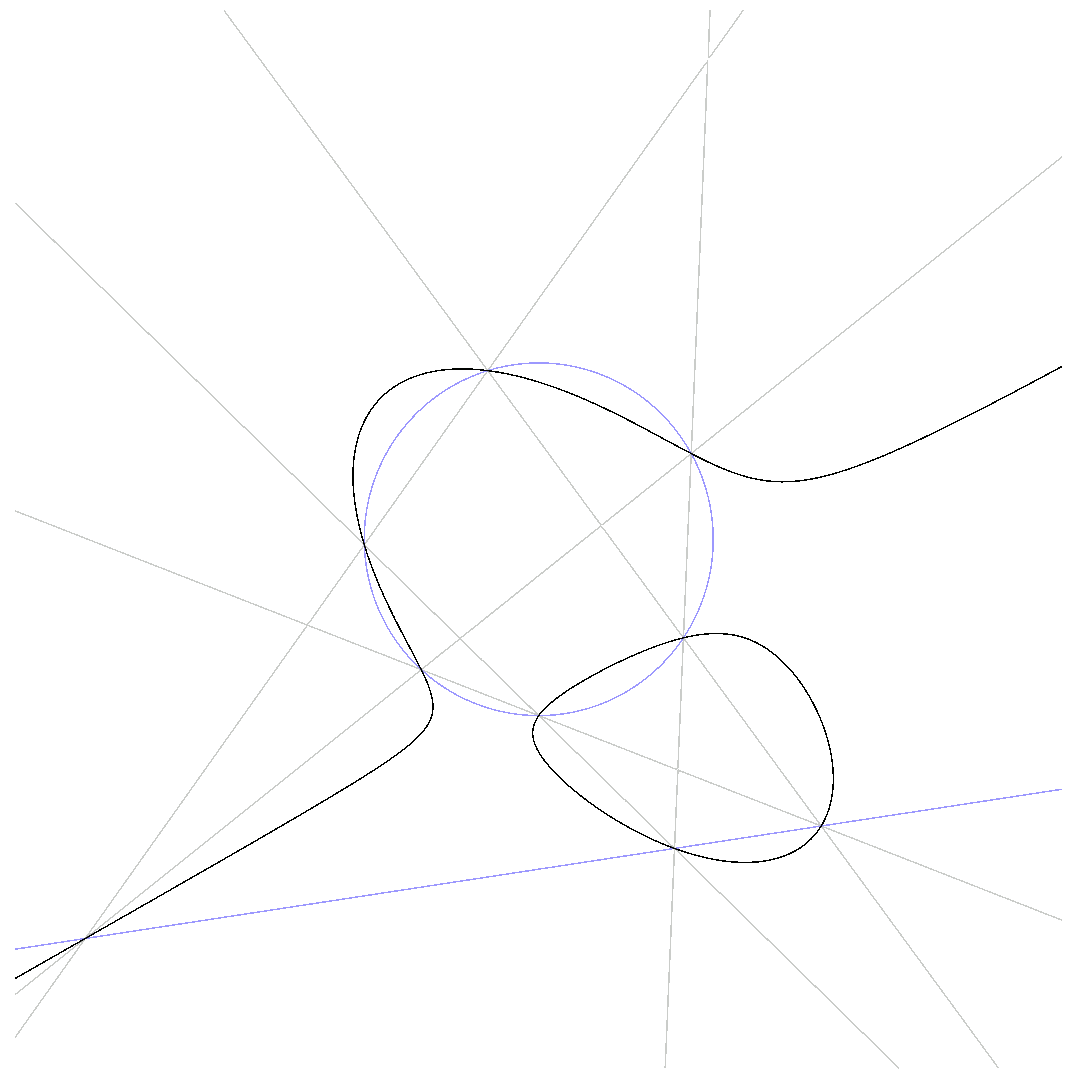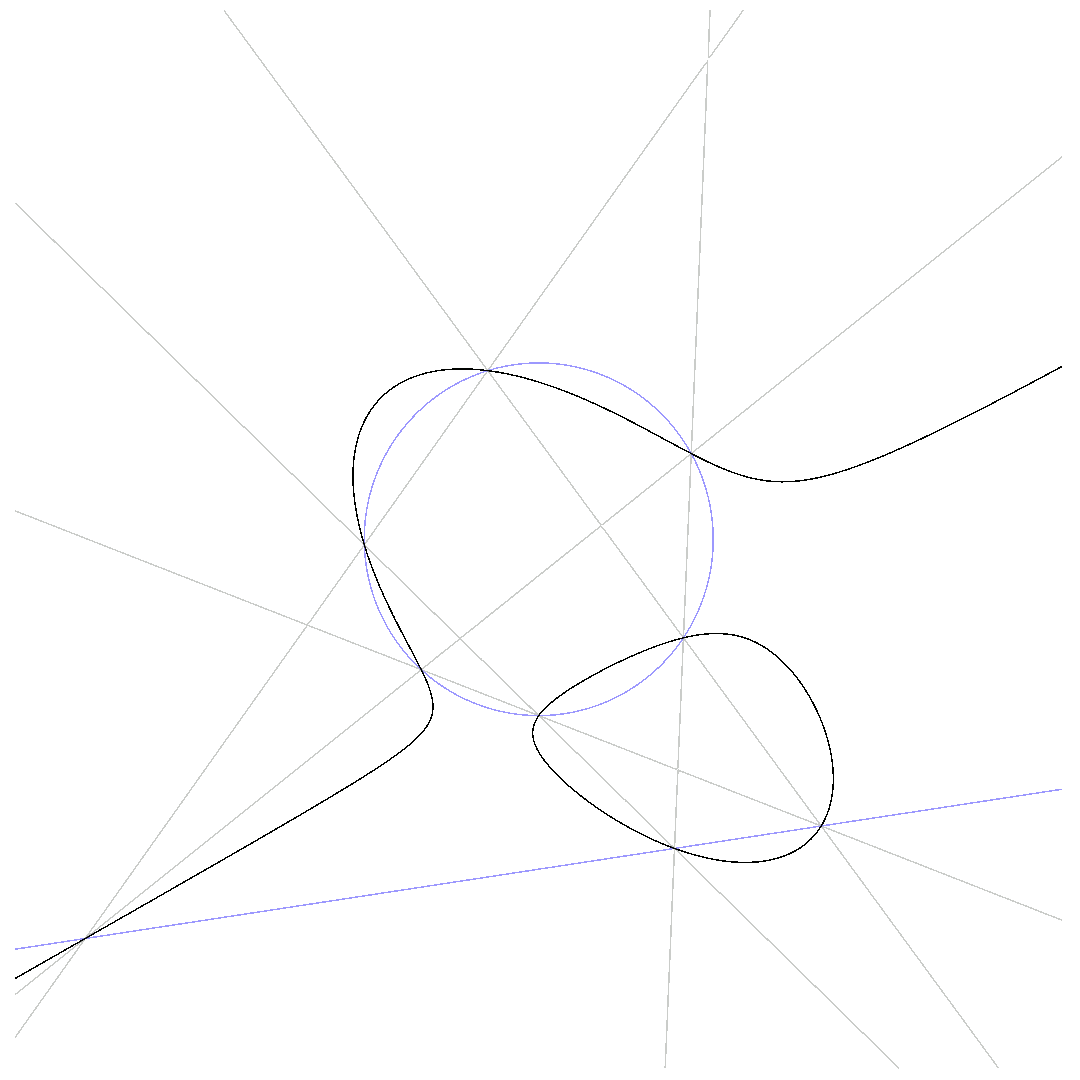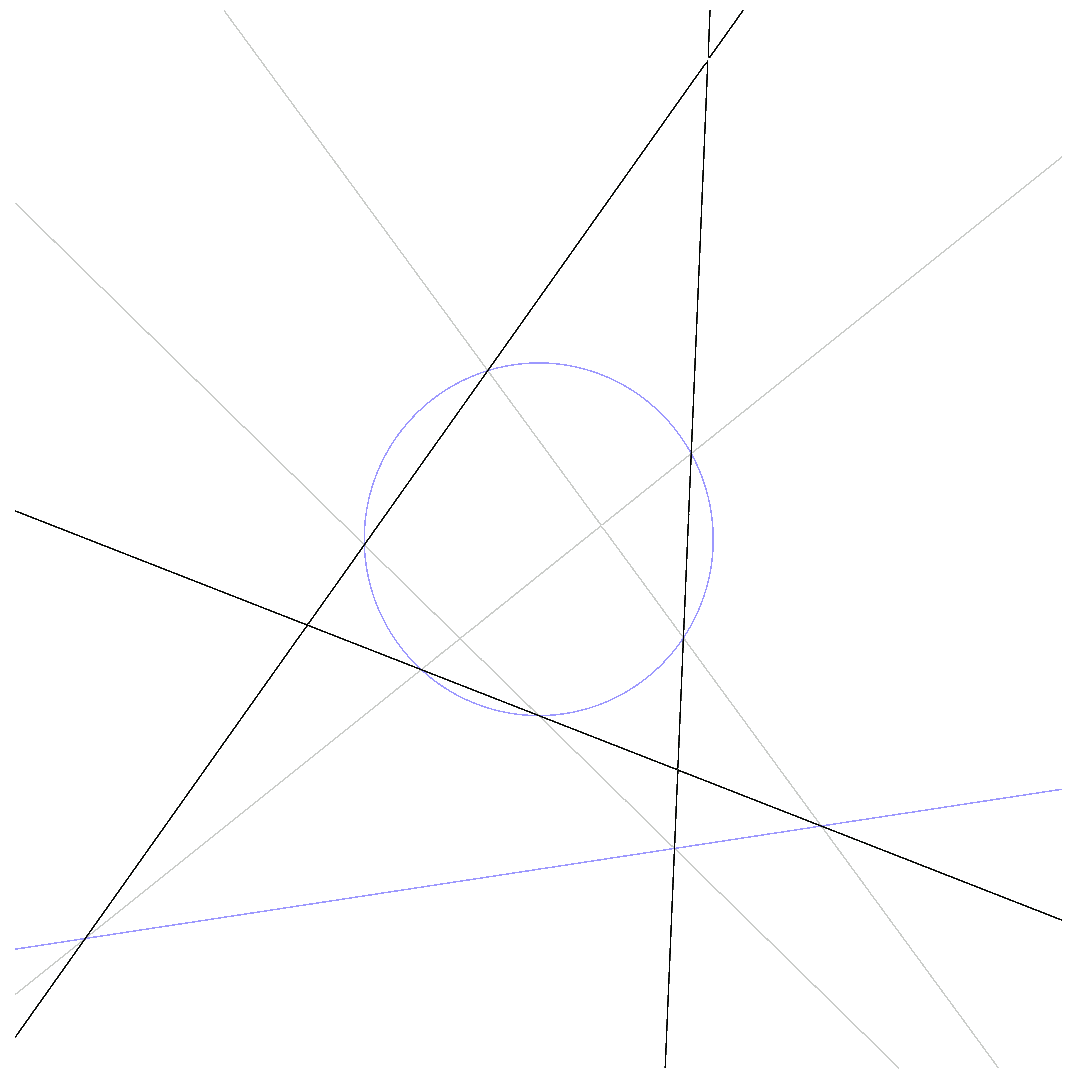
$\mbox{Pascal-line and conic do not intersect}$
We get a 5-point-Pascal, when two intersection-points, connected via one of the $6$ lines defining $p_1$ and $p_2$, coincide. Then, we have an intersection point with multiplicity $2$, or, in other words, one of the 6 lines is tangential to the conic.
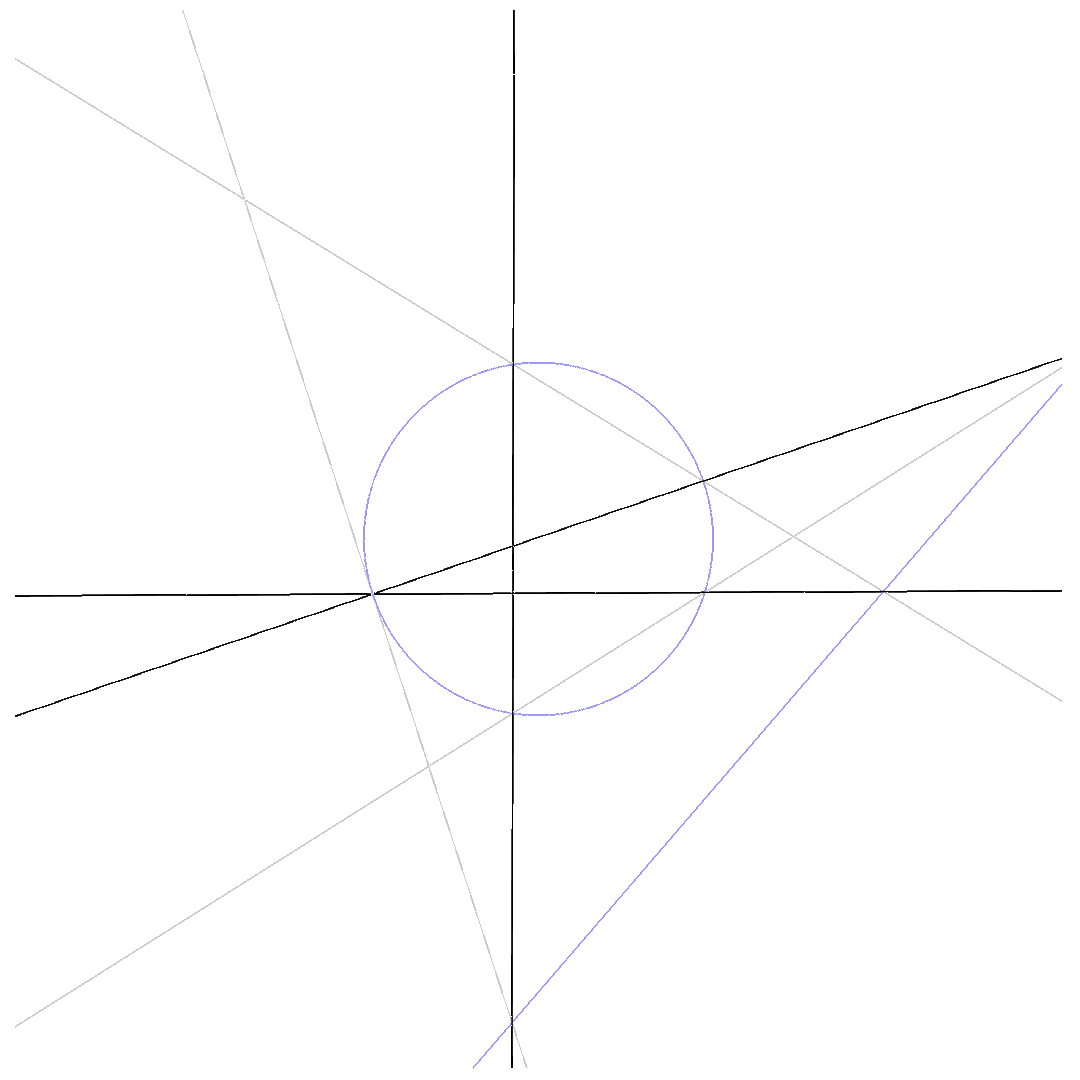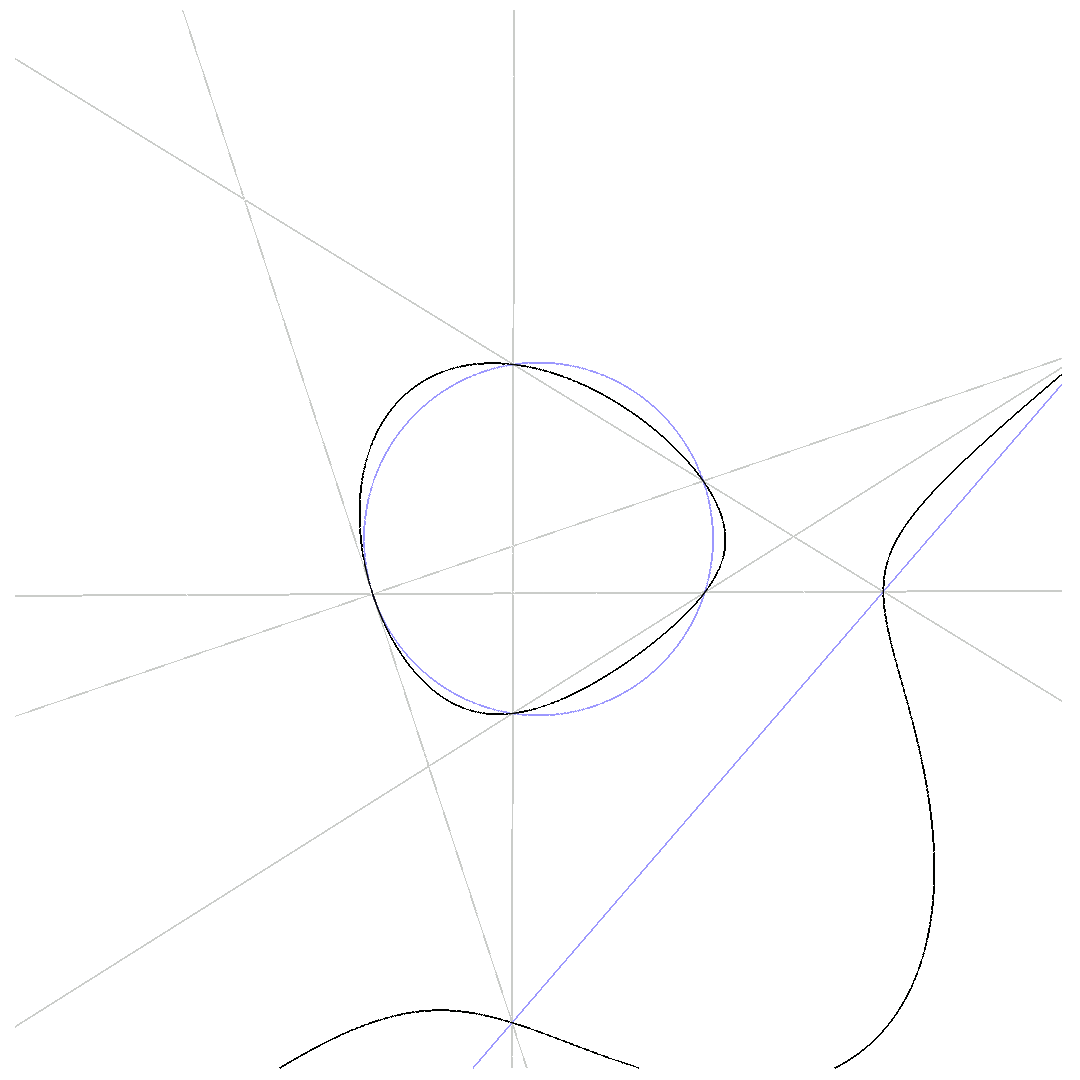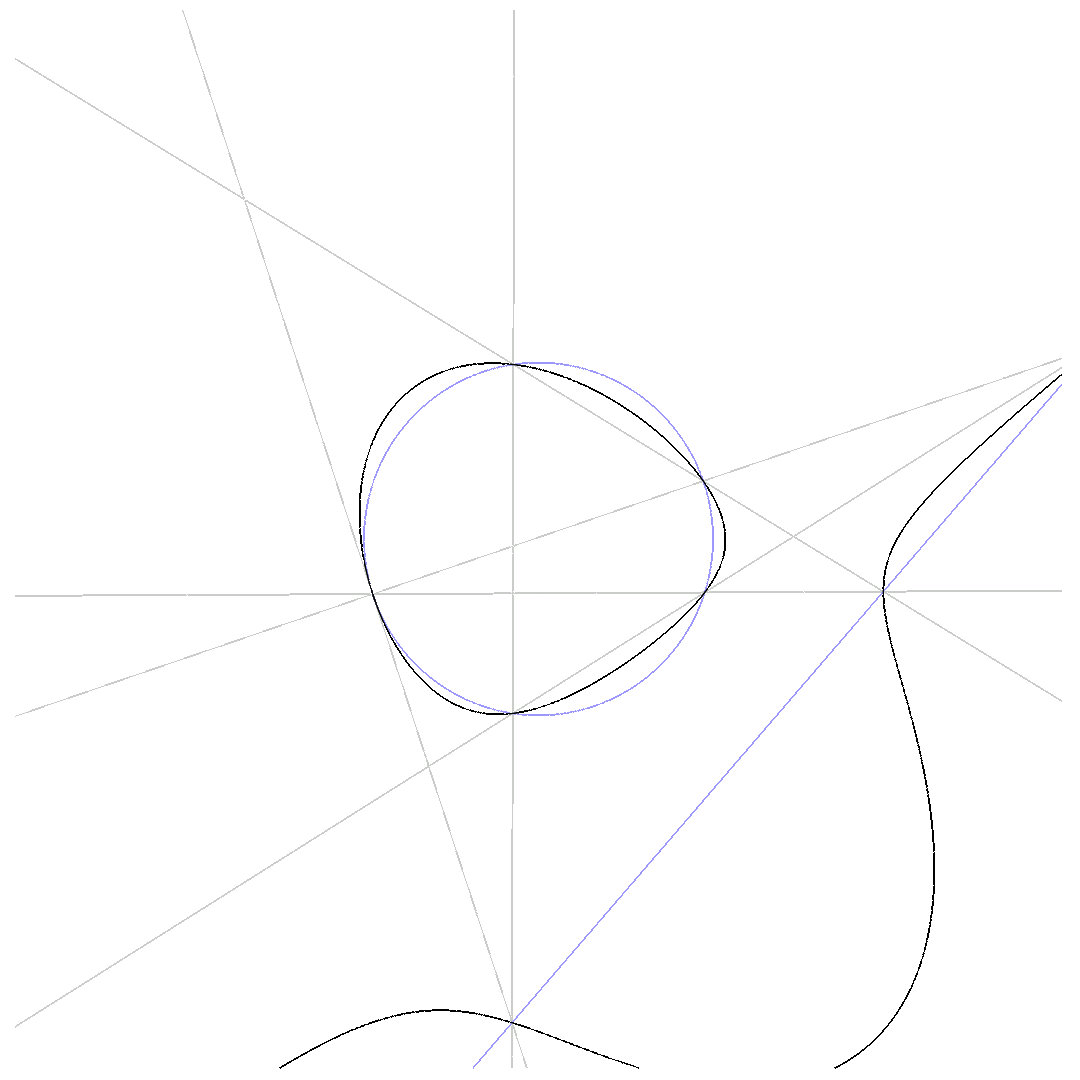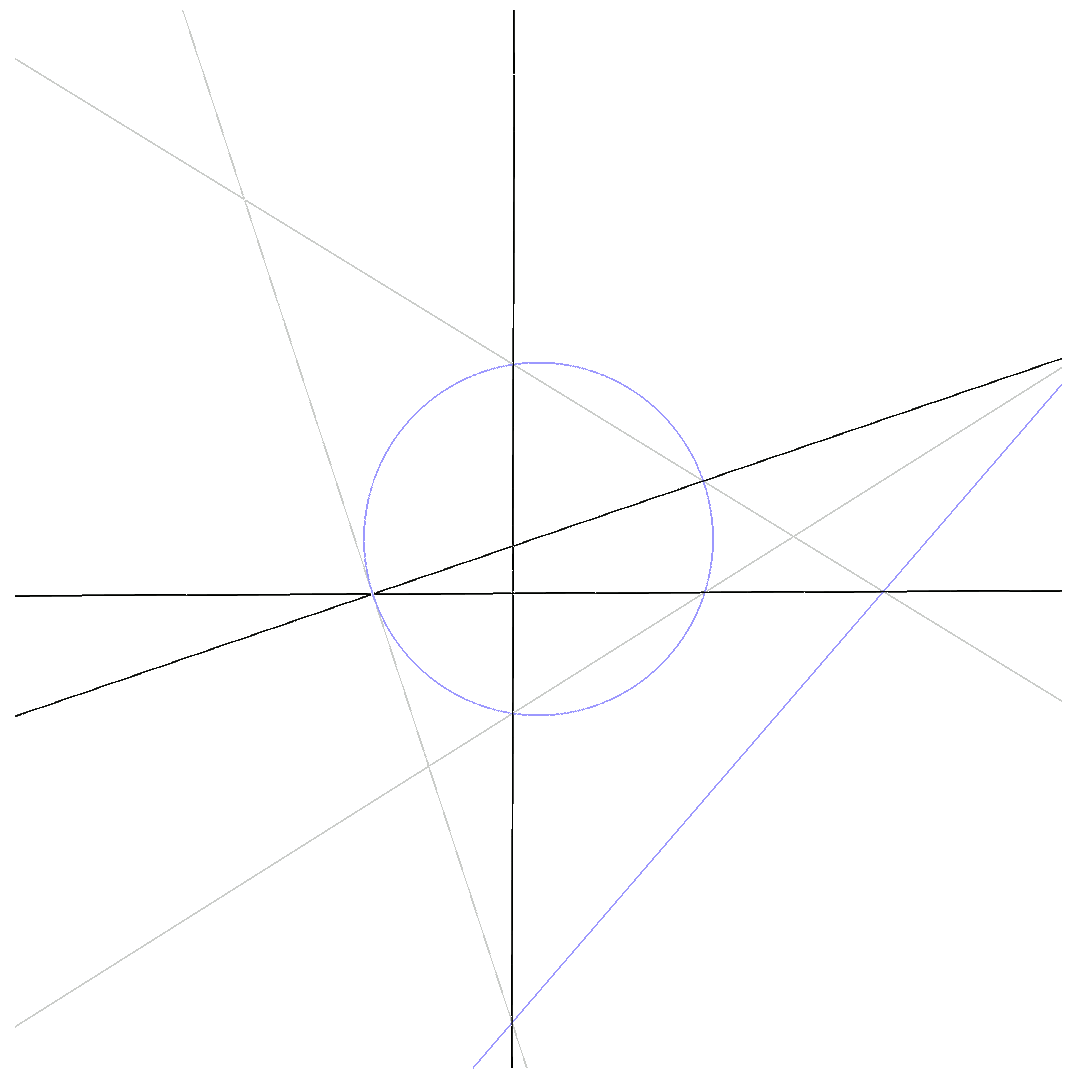
$\mbox{5-point-Pascal}$
Two of the 6 lines are tangential to the conic:
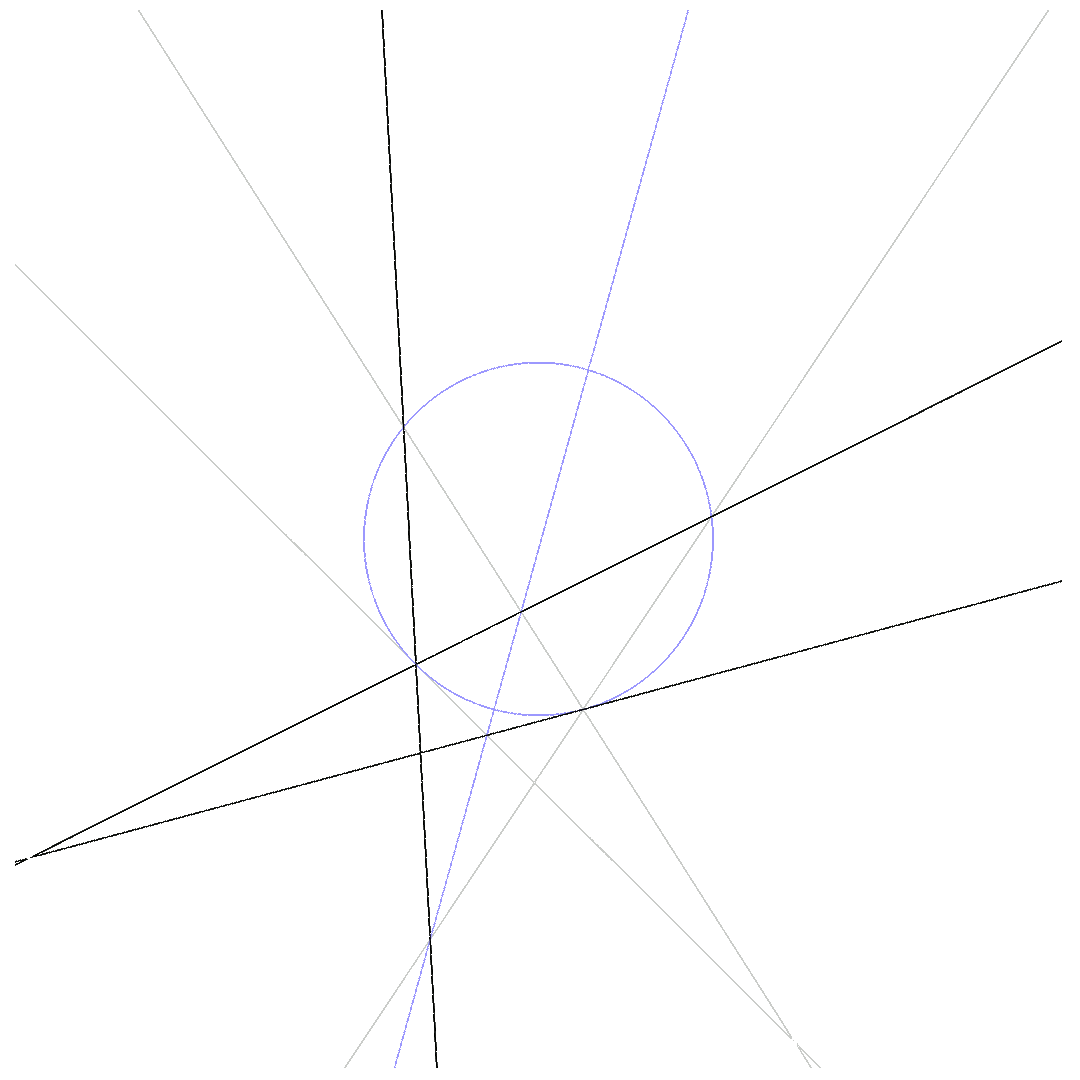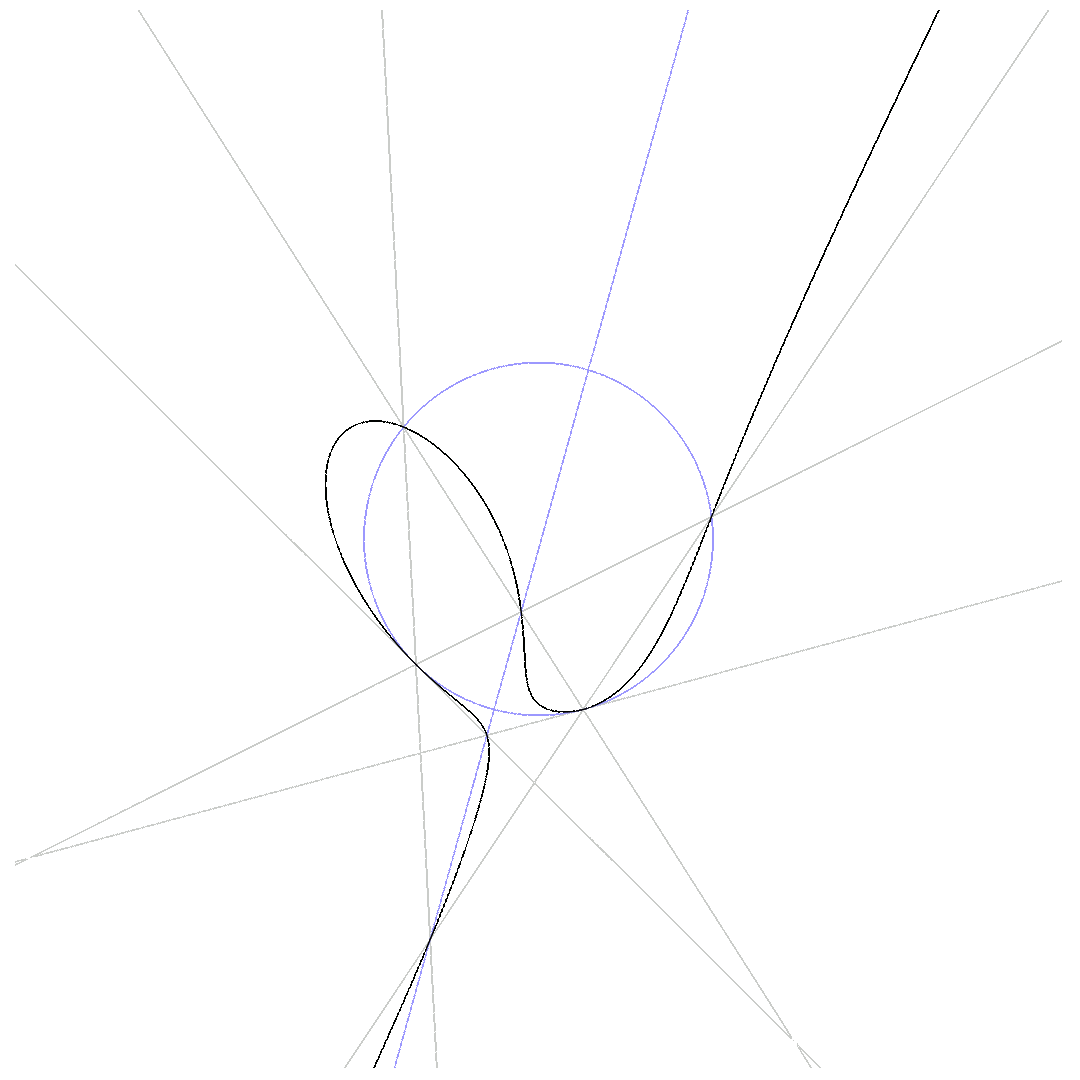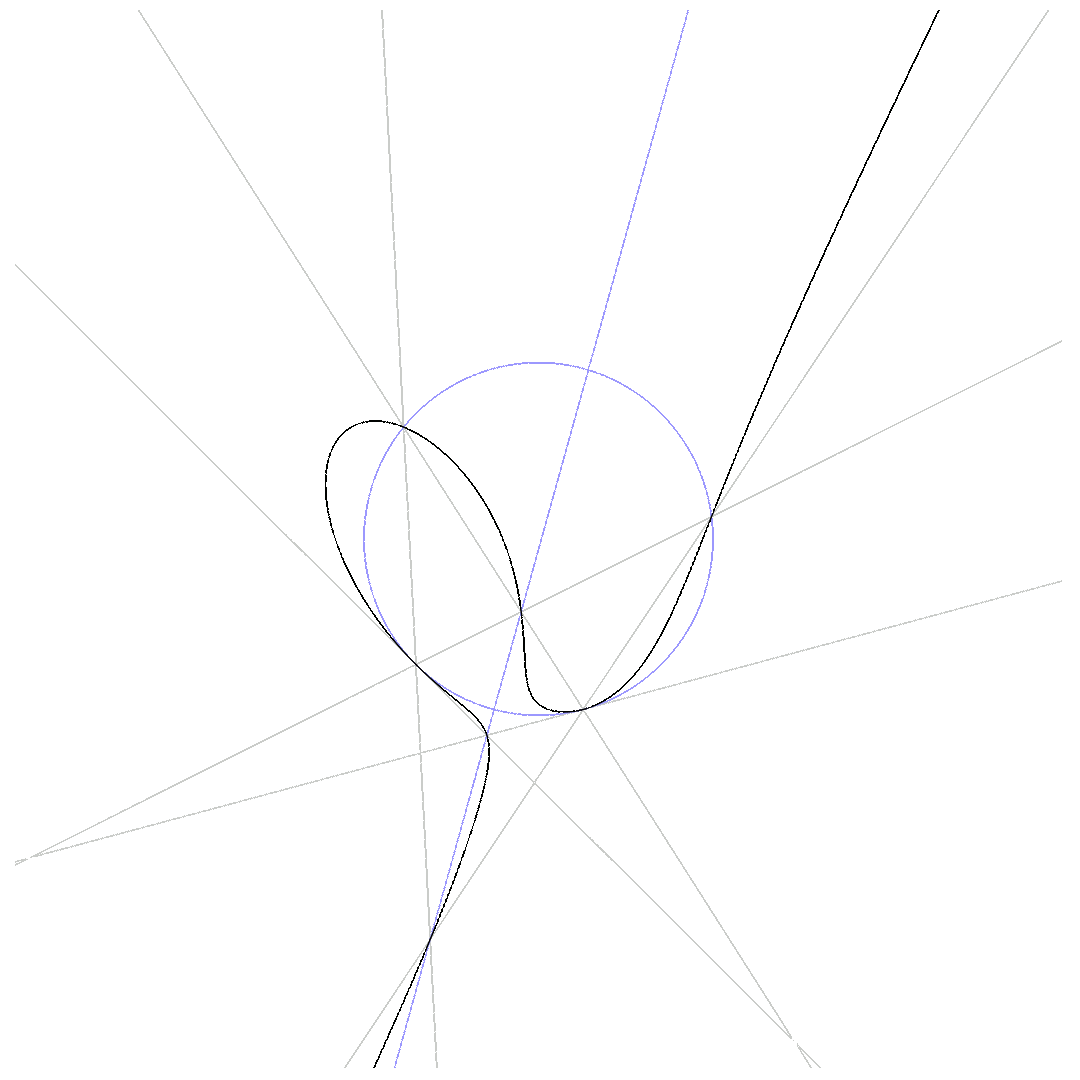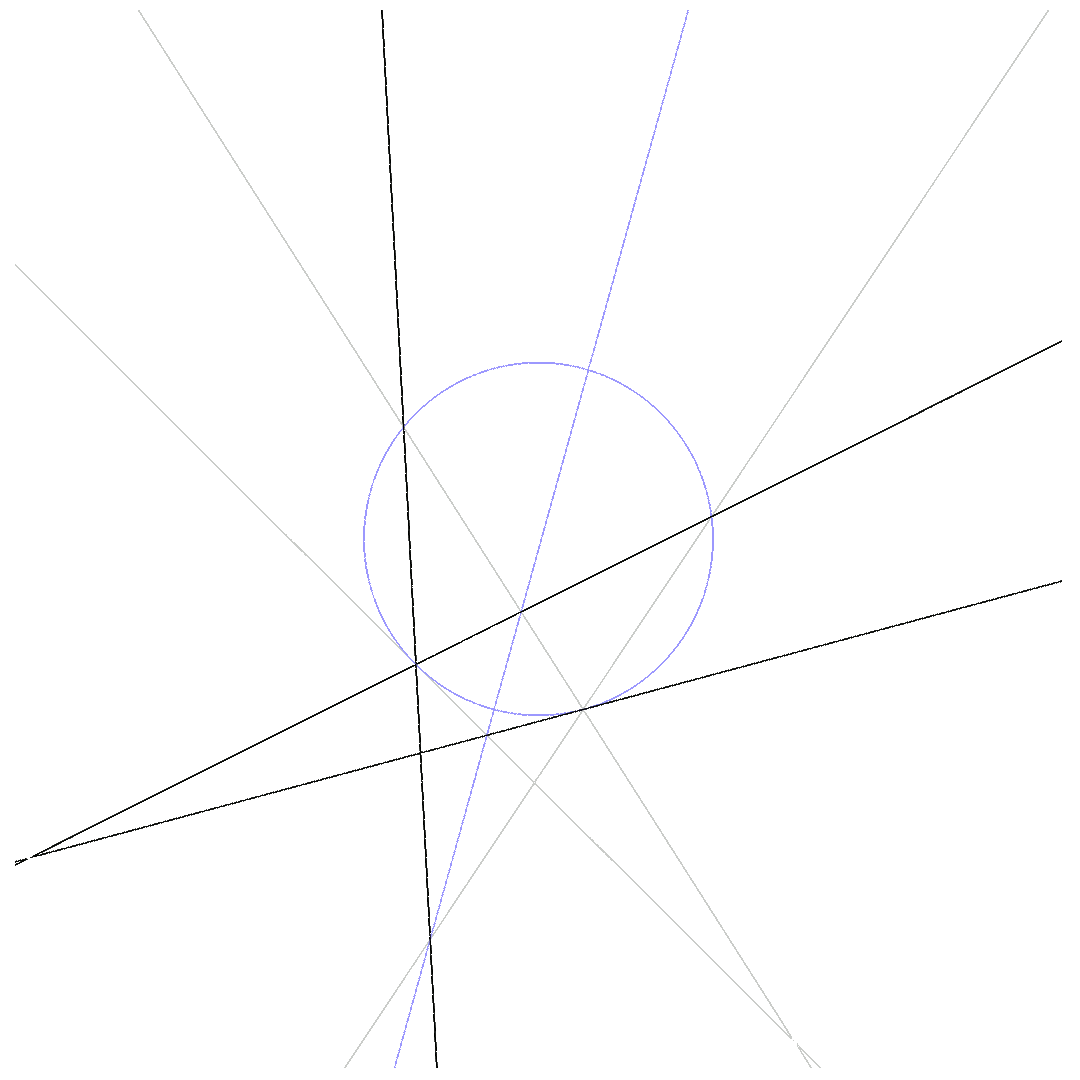
$\mbox{4-point-Pascal}$
Three of the 6 lines are tangential to the conic:
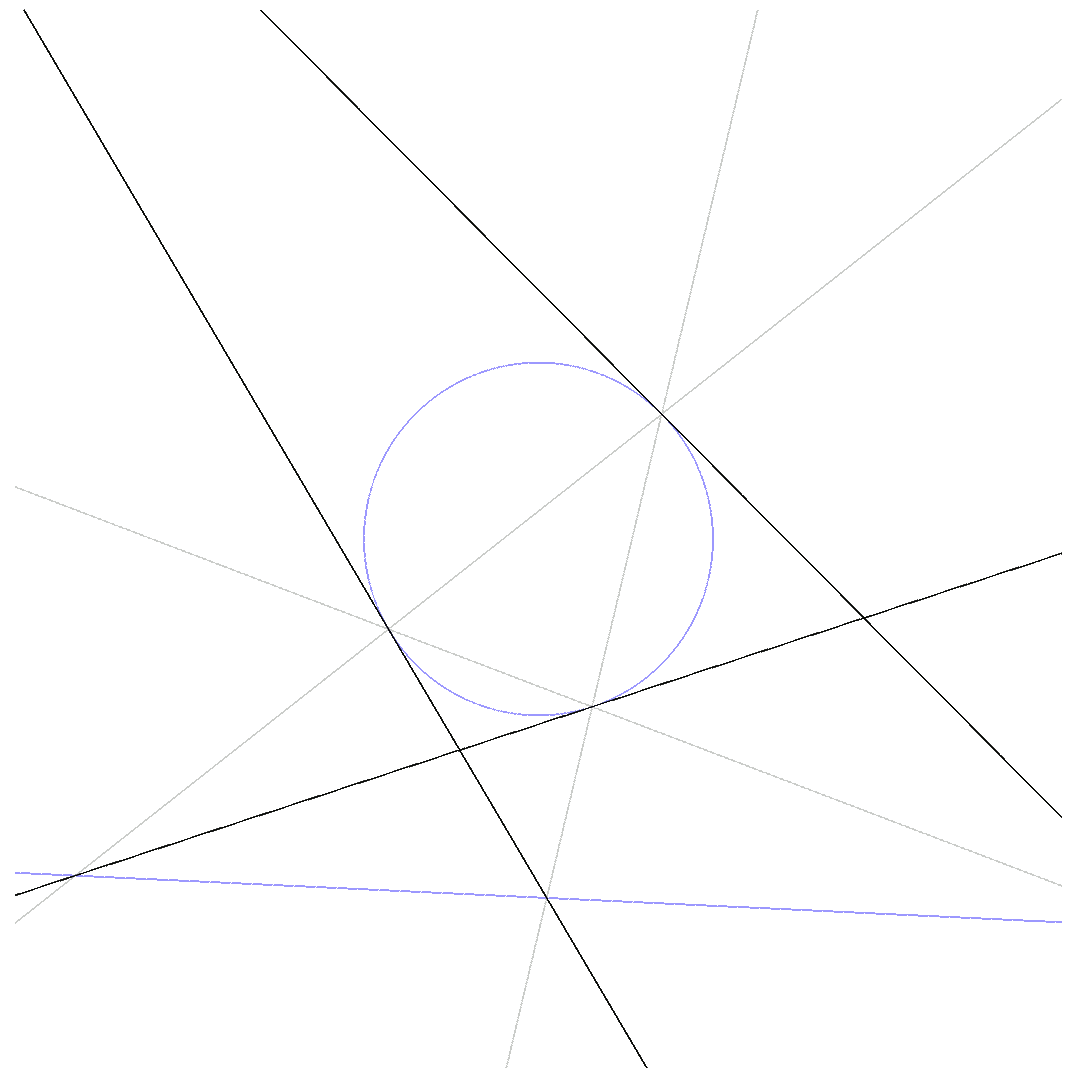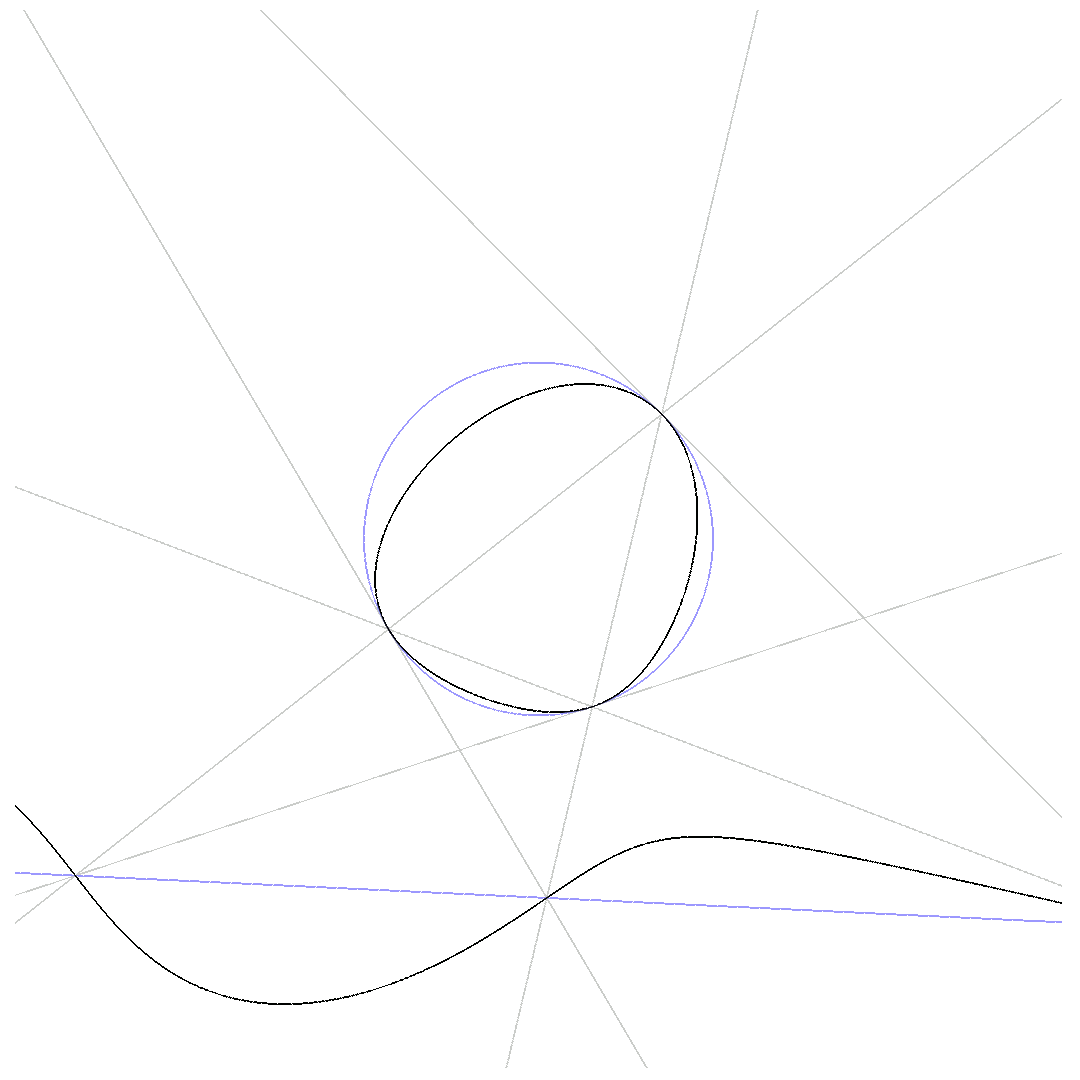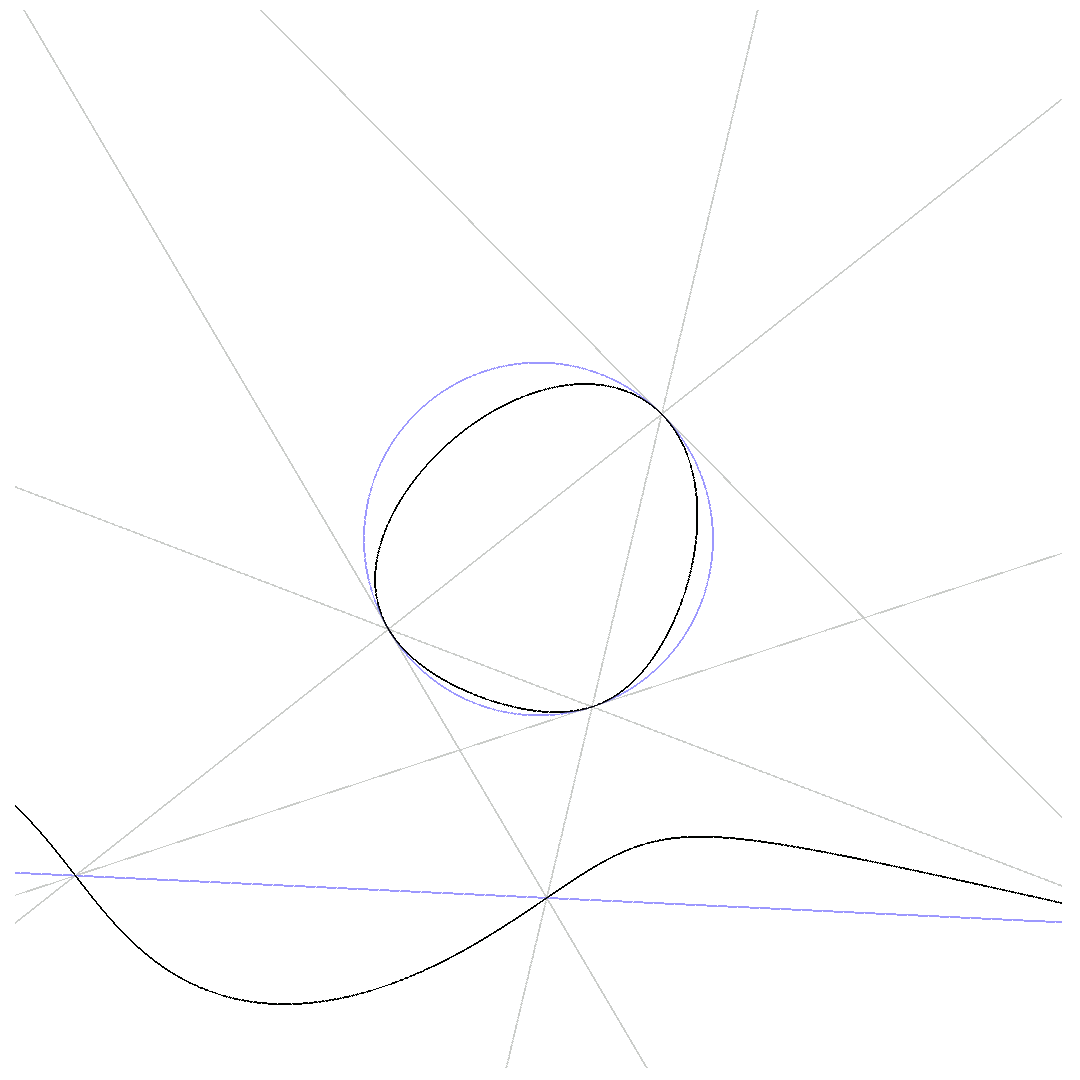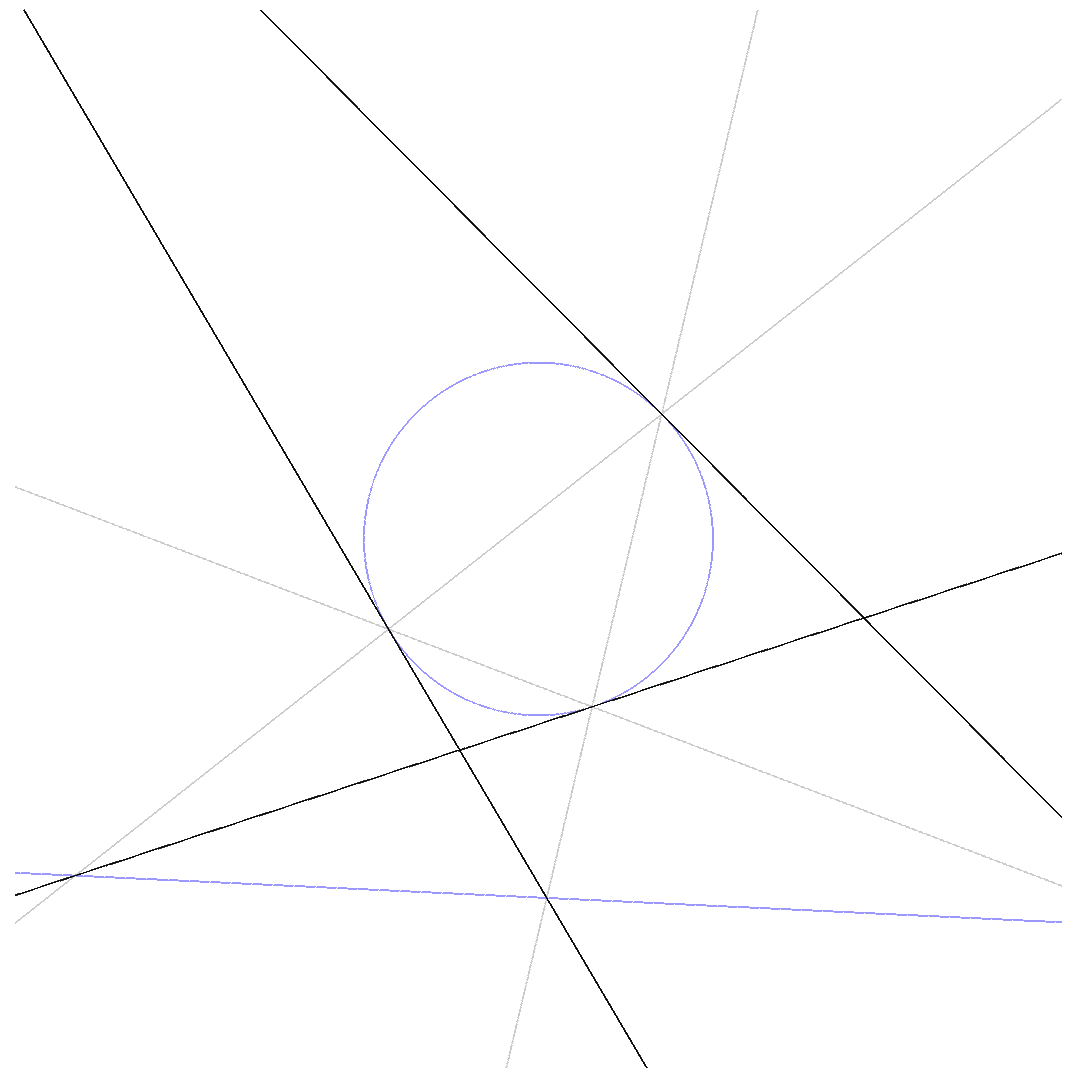
$\mbox{3-point-Pascal}$
Degenerated case: The cubics and the conic all share one linear component. This component is the Pascal-line and it is now tangential to the conic.